Modeling COVID-19 vaccination from a statistical perspective
Vaccination campaigns can be relatively simple to model from a statistical perspective. One reason is that vaccination campaigns typically proceed as designed by professionals, away from the media, and supported by a great deal of experience accumulated from years of repetition. In these conditions, sociological factors are expected to play a minor role. However, these conditions do not entirely hold in the case of COVID-19 for several reasons:
- Society is fully aware of the process, drawing the biggest mediatic attention in 2020 and 2021.
- Society is fragmented into groups with different views on vaccines, trying to influence each other's opinions.
- The vaccines are produced, delivered, and applied almost in real-time, so the vaccination dynamics must be coupled with production and delivery dynamics.
- The uncertainty in the conditions under which the vaccination is going to take place in a fastly evolving scenario of competition between countries and new virus variants
These points are the main reasons that make the COVID-19 vaccination campaign special from a statistical modeling perspective. In this post, I propose a statistical model reproducing the evolution of the ongoing COVID-19 vaccination campaign in specific countries. The model segments the population into agnostics, pro-, and anti-vaccines. Vaccination is modeled as a Poisson process, and social pressure on the population can change their views on vaccines (you can find a detailed explanation of the model at the end of this post). Moreover, the modeling approach naturally considers the model parameters' uncertainty, allowing users to forecast worst and best-case scenarios.
NOTE: This model's interactive web App version can be found here.
Before discussing model results, let's introduce the model parameters tuned to reproduce the real-world observations. You can find a more detailed explanation of the role of each of these parameters at the end of this post.
| Parameter | Description |
|---|---|
| % Pro-vaccines | Percentage of people that will take a vaccine as soon as possible |
| % Anti-vaccines | Percentage of people that will never take a vaccine |
| Strength of the social pressure | Controls the prob. that an agnostic becomes pro-vaccines |
| Initial stock | Amount of vaccines in stock at the beginning of the campaign |
| Duplication time | Time that the weekly-produced vaccines takes to double |
| Weekly arrival limit | Maximum amount of vaccines that can be produced/delivered per week |
The model considers ranges of plausible parameter values instead of single-point estimates. These intervals represent the uncertainty in a specific user's knowledge and thus will differ from user to user or country to country. For demonstration purposes, I arbitrarily set them here to illustrate the model results but always try to match the average. In the following plots, you can find examples of the model results tailored to reproduce the vaccination campaigns of different countries. The model results are in blue, where the shaded region contains 95% of the sampled data. The results are optimized to reproduce the real-world data (in red) of the vaccination campaigns in the USA, Germany, and Africa.
USA
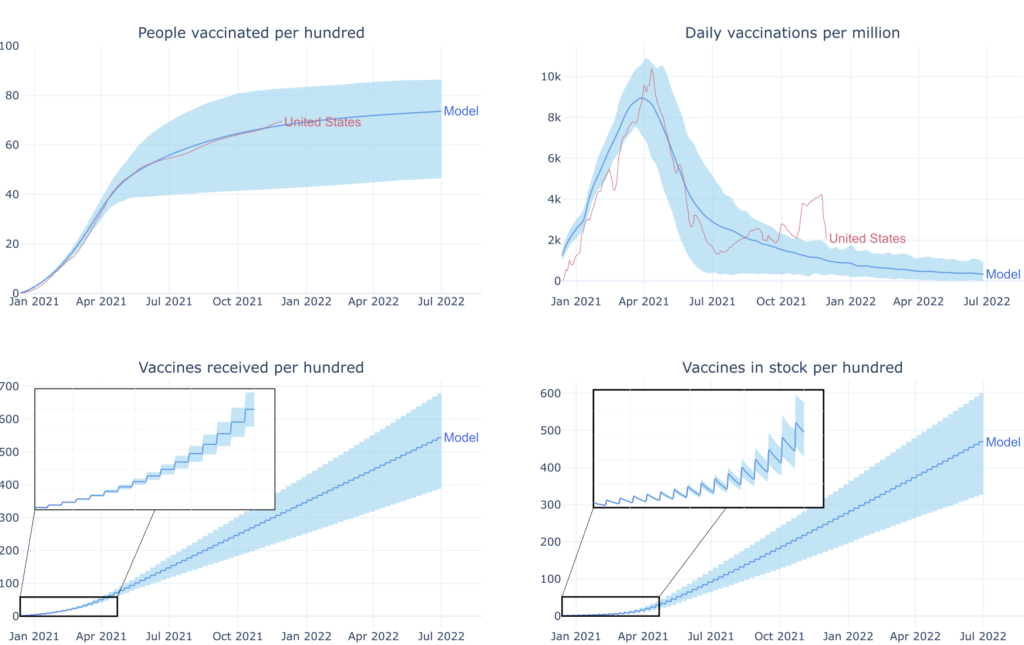
| Parameter | Value |
|---|---|
| Pro-vaccines | 35% - 40% |
| Anti-vaccines | 12% - 25% |
| Strength of the social pressure | 0 - 0.02 |
| Initial stock | 1% - 1.2% of the pop. |
| Duplication time | 5 - 7 weeks |
| Weekly arrival limit | 5% - 10% of the pop. |
Germany
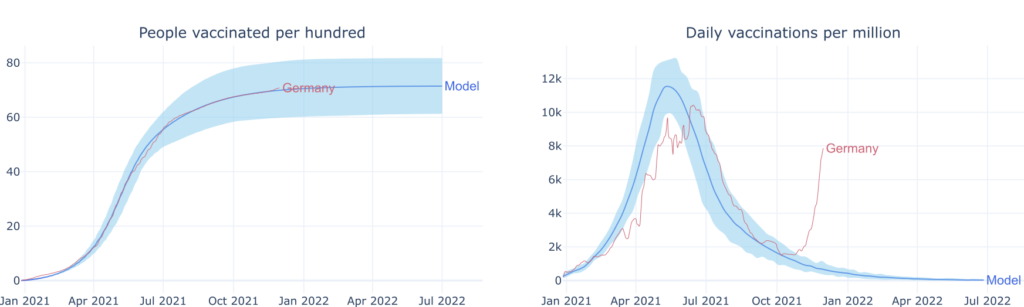
| Parameter | Value |
|---|---|
| Pro-vaccines | 35% - 40% |
| Anti-vaccines | 17% - 40% |
| Strength of the social pressure | 0.02 - 0.025 |
| Initial stock | 0.2% - 0.24% of the pop. |
| Duplication time | 3 - 4 weeks |
| Weekly arrival limit | 9.5% - 10% of the pop. |
Africa
In the case of Africa, I've followed a different approach since there's still not much data available. Specifically, since we have only observed the campaign's initial stages, it's difficult to say anything about the characteristics of the population. For example, the value at which the percentage of the vaccinated population saturates is controlled by the number of anti-vaccines. However, since we are still far from reaching such saturation, we cannot say much about this parameter. But is precisely in this situation that we can leverage the model's capabilities for handling uncertainty. Thus, we use the campaign's initial stages (i.e., the observed data) to more or less accurately establish the vaccine production and delivery parameters. Then, we consider a broad range of parameter values for the pro and anti-vaccine percentages and the social pressure. We don't commit to a specific value by proceeding in this way. Instead, we model a whole range of scenarios. This approach suggests (as of November 2021) that in the best-case scenario, Africa won't reach a vaccination level of 80% till at least summer 2022. In the worst-case scenario, the level will never be above 65%. In reality, something in-between will probably occur, such as a saturation level close to 75%, reaching by the end of 2022 or the beginning of 2023. We must note that we are using aggregated data for Africa. The reality is, of course, more complex since geographical differences exist within the continent regarding vaccine delivery and population characteristics.
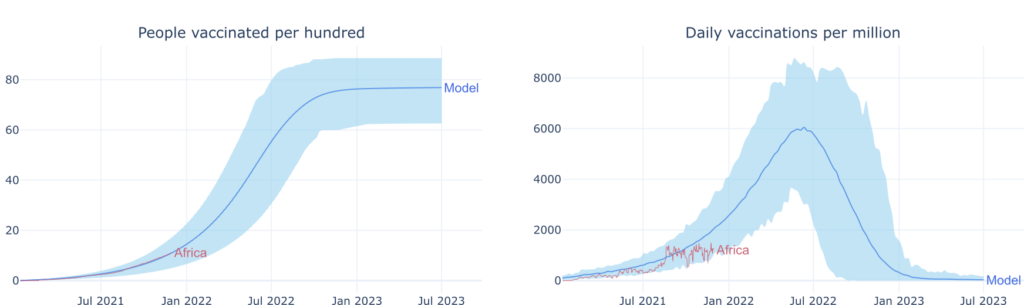
| Parameter | Value |
|---|---|
| Pro-vaccines | 50% - 90% |
| Anti-vaccines | 10% - 40% |
| Strength of the social pressure | 0.0 - 0.05 |
| Initial stock | 0.02% - 0.08% of the pop. |
| Duplication time | 11- 14 weeks |
| Weekly arrival limit | 9.5% - 10% of the pop. |
Future steps
The plots above evidence that this model can reproduce different vaccination campaigns with high fidelity if the model parameters are tuned adequately. Note that the discrepancy observed in the daily vaccinations after October 2021 is due to extra factors. The first was a sudden change in social pressure induced by a substantial rise in restrictions on non-vaccinated people. And second and more important, a reinforcing third dose is given to people who already got two doses. These factors could be straightforwardly accounted for in the model, e.g., letting the users specify parameter values as step functions over time. This would allow modeling fast changes in social pressure or in the number of vaccines that a person is asked to take by health authorities. For the sake of simplicity, these features have been so far left out. The question now is, what can the current model be used for?
There are several possibilities that we will explore in future blog posts. The first possibility is to perform a systematic optimization against data from different countries and then compare the best-fitting model parameters. This approach would provide us with interesting insights into the characteristics of the population of different countries. For example, the composition of the society (percentages of pro-, anti-vaccine, and agnostics) or the strength of social pressure. Plotting these values on a map might reveal interesting geographical trends. Thus, the model can be used to extract sociological insights from the data.
Another possibility is forecasting. Arguably, at this point, there is not much need for forecasting anymore, as could be the case at the beginning of 2021. Nonetheless, there are some important exceptions, such as in Africa, where the vaccination still has a long way to go. For example, for applying Bayesian forecasting, we need a model that helps us estimate the likelihood of the data, prior probability distributions on the parameters, and a Markov Chain Monte Carlo sampling algorithm such as Gibbs sampling. We already have a model that can reproduce reality well and the prior probability distributions (for simplicity, we assumed uniform distributions but can be easily generalized). For the sampling algorithm, we can leverage existing Python probabilistic programming libraries such as PyMC3. The sampling algorithm would allow us to estimate the posterior probability distribution for the parameters. The posterior distribution corresponds to our updated knowledge of the parameters in the light of the observed data, given the model. With the posterior distribution, we can compute the so-called posterior predictive distribution, which corresponds to the Bayesian prediction for the vaccination values at future times where no observed data is available yet.
This work will be continued in future blog posts.
The model
You can find a Python implementation of the model in this repository. In the README file, you can find detailed instructions on how to run it. Alternatively, you can interact with the model through this web App instead of running it on your machine. The model works as follows:
Population segments
We consider a population of size ![]() segmented into three groups, depending on their views on vaccines:
segmented into three groups, depending on their views on vaccines:
- Pro-vaccines: they take the vaccine as soon as they have the chance
- Anti-vaccines: they will never take a vaccine
- Agnostics: they initially hesitate, but given enough social pressure, they will take it
The size of each group is given by ![]() ,
, ![]() and
and ![]() , with
, with ![]() . We will denote the number of vaccinated people by
. We will denote the number of vaccinated people by ![]() and the number of people currently waiting for a dose by
and the number of people currently waiting for a dose by ![]() . The latter refers to people who want to get a dose but didn't do it yet.
. The latter refers to people who want to get a dose but didn't do it yet.
Vaccination dynamics
The following three steps are applied daily:
1. Production and delivery of new doses
The day number ![]() is increased by a unit,
is increased by a unit, ![]() . On the first day of each week, the number of newly arriving vaccines
. On the first day of each week, the number of newly arriving vaccines ![]() is computed as
is computed as
![]()
where ![]() grows exponentially with
grows exponentially with ![]() to meet very high demand. In this expression,
to meet very high demand. In this expression, ![]() is the number of doses in stock at the beginning of the campaign. The factor
is the number of doses in stock at the beginning of the campaign. The factor ![]() in this expressions means that
in this expressions means that ![]() is the duplication time in weeks (i.e., the number weeks it takes for the production of vaccines to increase by a factor of two,
is the duplication time in weeks (i.e., the number weeks it takes for the production of vaccines to increase by a factor of two, ![]() if
if ![]() ). Since
). Since ![]() cannot grow indefinitely, it is throttled at a maximum weekly delivery capacity
cannot grow indefinitely, it is throttled at a maximum weekly delivery capacity ![]() . Thus,
. Thus,
![]()
The number of doses in stock, ![]() is then updated as
is then updated as
![]()
2. Vaccination of people that is waiting for it
The number of people vaccinated in one day, ![]() is a Poisson random variable with parameter
is a Poisson random variable with parameter ![]() , where
, where ![]() is the probability that a person has the vaccine available. The factor 2/7 accounts for vaccinations occurring only two days a week, giving an effective per-day probability. We must take into account that the number of vaccines applied on a day cannot exceed the number of doses in stock nor the number of people currently waiting to be vaccinated, thus
is the probability that a person has the vaccine available. The factor 2/7 accounts for vaccinations occurring only two days a week, giving an effective per-day probability. We must take into account that the number of vaccines applied on a day cannot exceed the number of doses in stock nor the number of people currently waiting to be vaccinated, thus
![]()
Then, the number of vaccinated persons, vaccines in stock, and people currently waiting for a vaccine are updated as,
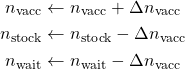
3. Social pressure on the agnostics
The number of agnostic people that change their mind and decide to get vaccinated, ![]() , is a Poisson random variable with parameter
, is a Poisson random variable with parameter ![]() . The probability
. The probability ![]() is that of an agnostic person changing their mind during a day, and is approximated by
is that of an agnostic person changing their mind during a day, and is approximated by ![]() . The term
. The term ![]() acts as a proxy for social pressure. Specifically, the higher the fraction of the vaccinated population, the higher the pressure on the agnostics to do the same. The factor
acts as a proxy for social pressure. Specifically, the higher the fraction of the vaccinated population, the higher the pressure on the agnostics to do the same. The factor ![]() allows tuning the strength of this effect. The value of
allows tuning the strength of this effect. The value of ![]() emerges from complex social dynamics beyond the scope of this model. Thus, its value can only be determined during a model training step. We must take into account that the number of conversions cannot overcome the current number of agnostics, thus
emerges from complex social dynamics beyond the scope of this model. Thus, its value can only be determined during a model training step. We must take into account that the number of conversions cannot overcome the current number of agnostics, thus
![]()
Then, the number of agnostics and waiting people are updated as,
![]()
Initial values
The values of the variables during the first day, i.e., at ![]() are,
are,
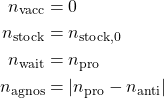
Sampling the model's parameter space
The model is sampled a number ![]() of times, where each sample corresponds to applying the three steps above until reaching a maximum number of days. The model's free parameters are the initial stock of vaccines
of times, where each sample corresponds to applying the three steps above until reaching a maximum number of days. The model's free parameters are the initial stock of vaccines ![]() , the vaccines duplication time in weeks
, the vaccines duplication time in weeks ![]() , the maximum weekly delivery capacity
, the maximum weekly delivery capacity ![]() , the prevalence of pro- and anti-vaccines,
, the prevalence of pro- and anti-vaccines, ![]() and
and ![]() respectively, and the social pressure parameter
respectively, and the social pressure parameter ![]() .
.
As discussed above, in a realistic situation, specifically during the initial stages of the COVID-19 vaccination campaign, the uncertainty in the model parameters can be considerable. Moreover, even if reasonable estimations could be made, it's still advisable to work with a range of values representing the best and worst-case scenarios for safety. To include the uncertainty in the parameters, we consider them as distributed according to specific probability distributions. Thus, we first draw the parameters from each simulated sample from these distributions. For simplicity, we consider each parameter uniformly distributed between an upper and a lower bound, which are specific for each parameter. In order to draw values of ![]() and
and ![]() such that
such that ![]() , rejection sampling is used.
, rejection sampling is used.
The value of the population size ![]() deserves particular comment.
deserves particular comment. ![]() must be set before sampling as a free parameter. However, it does not necessarily need to mimic a real country. For low
must be set before sampling as a free parameter. However, it does not necessarily need to mimic a real country. For low ![]() , the model will yield results with higher across-sample variability. As
, the model will yield results with higher across-sample variability. As ![]() increases, that variability drops. If we aim at simulating a small population, the value of
increases, that variability drops. If we aim at simulating a small population, the value of ![]() must be set accordingly. However, suppose we simulate a country with millions of citizens. In that case, the specific value of
must be set accordingly. However, suppose we simulate a country with millions of citizens. In that case, the specific value of ![]() does not matter much, as long as
does not matter much, as long as ![]() is big enough. A value of
is big enough. A value of ![]() already yields results similar to higher values. During the sampling procedure,
already yields results similar to higher values. During the sampling procedure, ![]() is the same for every sample.
is the same for every sample.
After the ![]() samples have been completed, we compute, for each day, the cross-sample average of different quantities. Specifically, we consider the fraction of the population vaccinated, daily doses applied, the total number of doses received by the country, and the current number of doses in stock. Moreover, we also give confidence intervals for each of these quantities by computing the across-sample
samples have been completed, we compute, for each day, the cross-sample average of different quantities. Specifically, we consider the fraction of the population vaccinated, daily doses applied, the total number of doses received by the country, and the current number of doses in stock. Moreover, we also give confidence intervals for each of these quantities by computing the across-sample ![]() and
and ![]() quantiles, where
quantiles, where ![]() defines the fraction of data
defines the fraction of data
that lies within the interval.
Related links
- An interactive web App version: https://covid19-vaccination-app.dfcastellanos.com
- The repository with the source code of the web App and the model back-end: https://github.com/dfcastellanos/COVID19-Vaccination-Model
- Real-world data: https://github.com/owid/covid-19-data
